ICML 2025

LangDAug is a Langevin-based data augmentation method for improving domain generalization in 2D medical image segmentation. It leverages Energy-Based Models (EBMs) trained via contrastive divergence to generate intermediate samples that bridge source domains using Langevin Dynamics. These samples act as natural augmentations, improving generalization to unseen domains.
We show that LangDAug provides a regularizing effect, theoretically bounding model complexity by the intrinsic dimensionality of the data manifold. Empirically, it outperforms state-of-the-art methods on retinal fundus and prostate MRI segmentation tasks, and complements domain-randomization strategies effectively.
Given multiple source domains , each associated with a distribution over the input-output space , the standard Empirical Risk Minimization (ERM) objective seeks to find model parameters that minimize the average loss over all training samples:
where denotes the total number of training samples aggregated from all source domains. However, ERM often fails to generalize to an unseen target domain , as it only optimizes performance over the observed source domains.
To bridge domains, we train an EBM to model the energy between domain pairs . The model is trained using Contrastive Divergence:
Sampling from is done using Langevin Dynamics with the chain being initialized at a point :
These LD iterates form samples that interpolate between domains.
We use the intermediate LD samples as augmentation data. For each sample , LD is run for steps to generate :
These samples, combined with original labels , are used in ERM training, effectively expanding the domain support:
LangDAug acts as a regularizer on the ERM objective. Let be the Langevin-perturbed sample. Then the augmented empirical risk is:
This can be decomposed as:
Where are regularization terms involving the first and second derivatives of the model , encouraging smoother and flatter solutions.
| Method | Domain A | Domain B | Domain C | Domain D | Avg mIoU | Avg mDSC |
|---|---|---|---|---|---|---|
| Hutchinson | 66.73 | 66.73 | 69.36 | 66.73 | 67.39 | 78.14 |
| MixStyle | 80.76 | 67.69 | 79.79 | 77.09 | 76.33 | 85.58 |
| FedDG | 76.65 | 72.14 | 76.10 | 75.96 | 75.21 | 83.67 |
| RAM | 77.42 | 73.79 | 79.66 | 78.74 | 77.40 | 85.39 |
| TriD | 80.92 | 72.45 | 79.34 | 78.96 | 77.92 | 85.95 |
| LangDAug (Ours) | 78.79 | 75.05 | 81.01 | 80.51 | 78.84 | 87.61 |
| Method | Domain A | Domain B | Domain C | Domain D | Domain E | Domain F | Avg ASD | Avg DSC |
|---|---|---|---|---|---|---|---|---|
| Hutchinson | 3.28 | 1.48 | 2.07 | 3.98 | 2.78 | 1.64 | 2.54 | 78.62 |
| MixStyle | 0.72 | 0.88 | 1.62 | 0.65 | 1.59 | 0.51 | 1.00 | 86.27 |
| FedDG | 1.09 | 0.93 | 1.31 | 0.88 | 1.73 | 0.50 | 1.07 | 85.95 |
| RAM | 0.93 | 0.98 | 1.26 | 0.74 | 1.78 | 0.32 | 1.00 | 87.02 |
| TriD | 0.70 | 0.72 | 1.39 | 0.71 | 1.43 | 0.46 | 0.90 | 87.68 |
| LangDAug (Ours) | 0.58 | 0.64 | 1.21 | 0.57 | 1.49 | 0.38 | 0.81 | 89.16 |
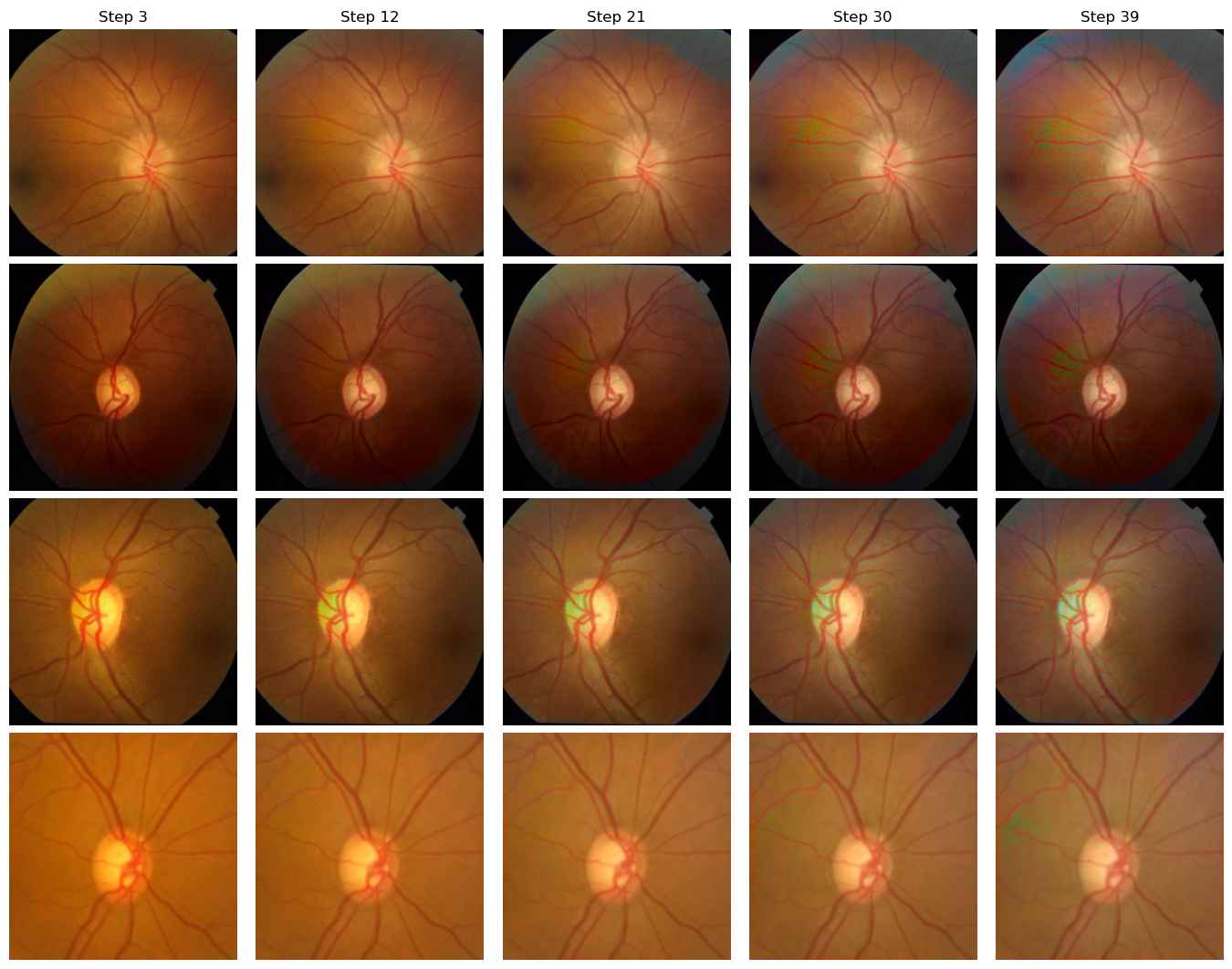
Domain A to Domain D
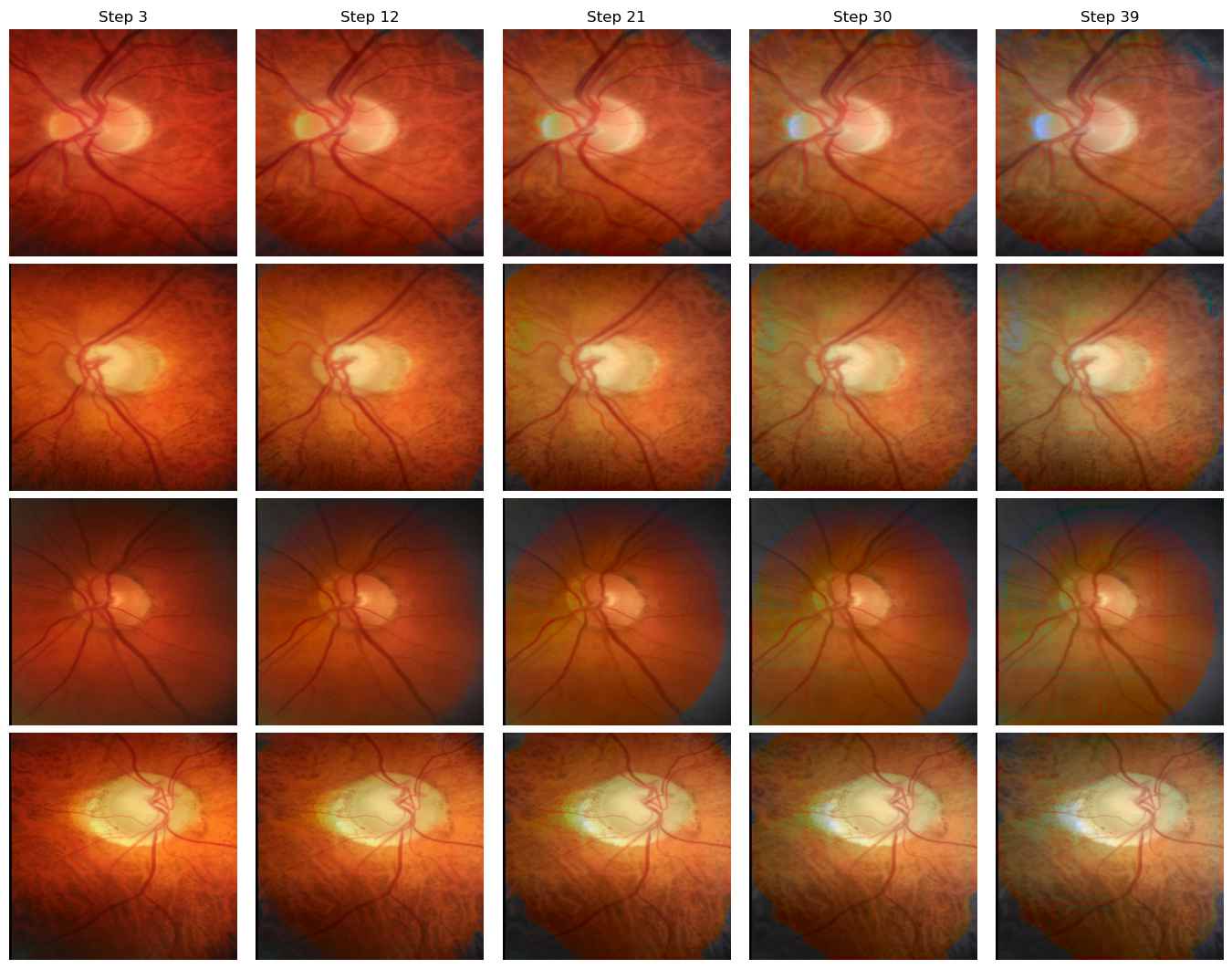
Domain B to Domain D
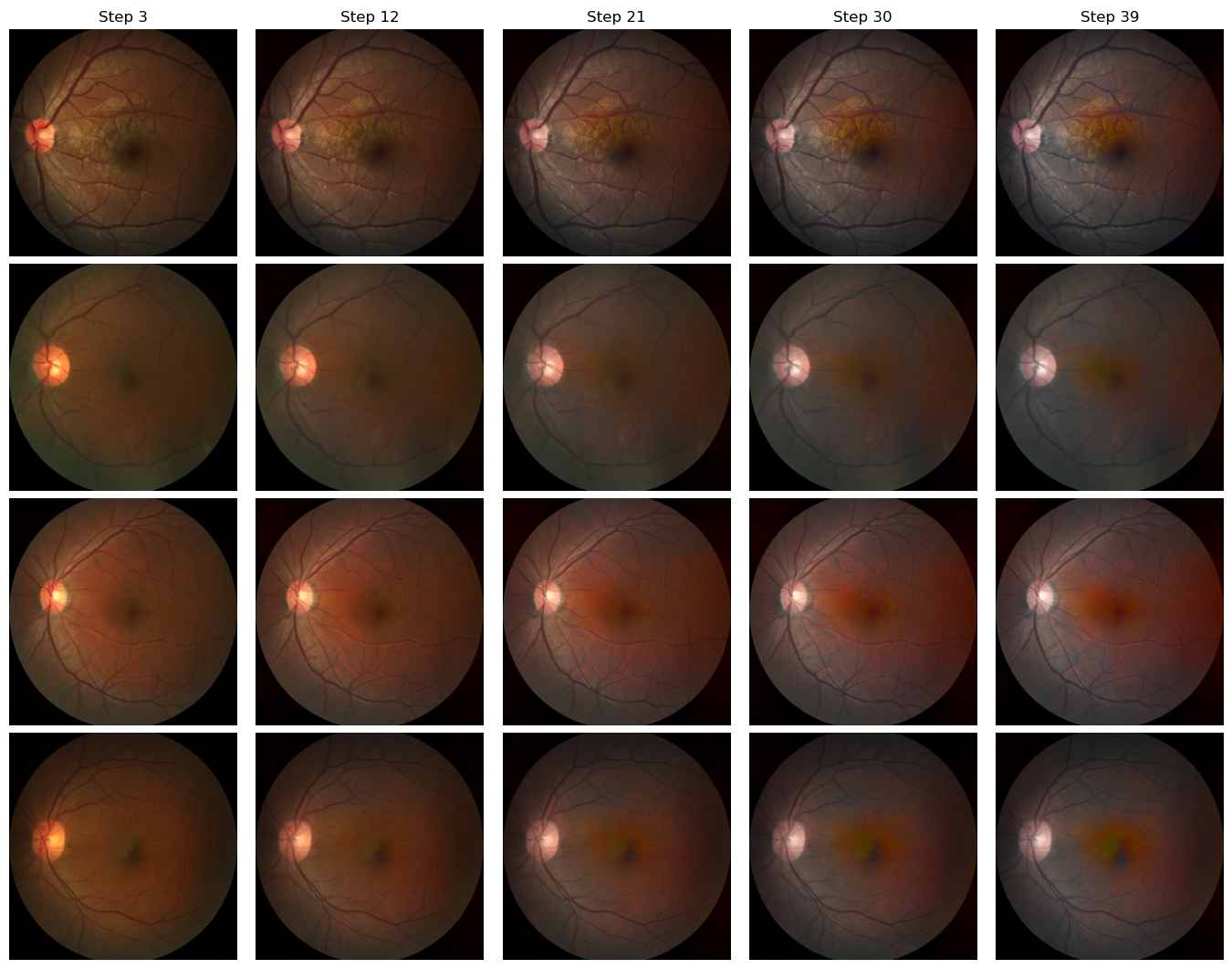
Domain C to Domain B
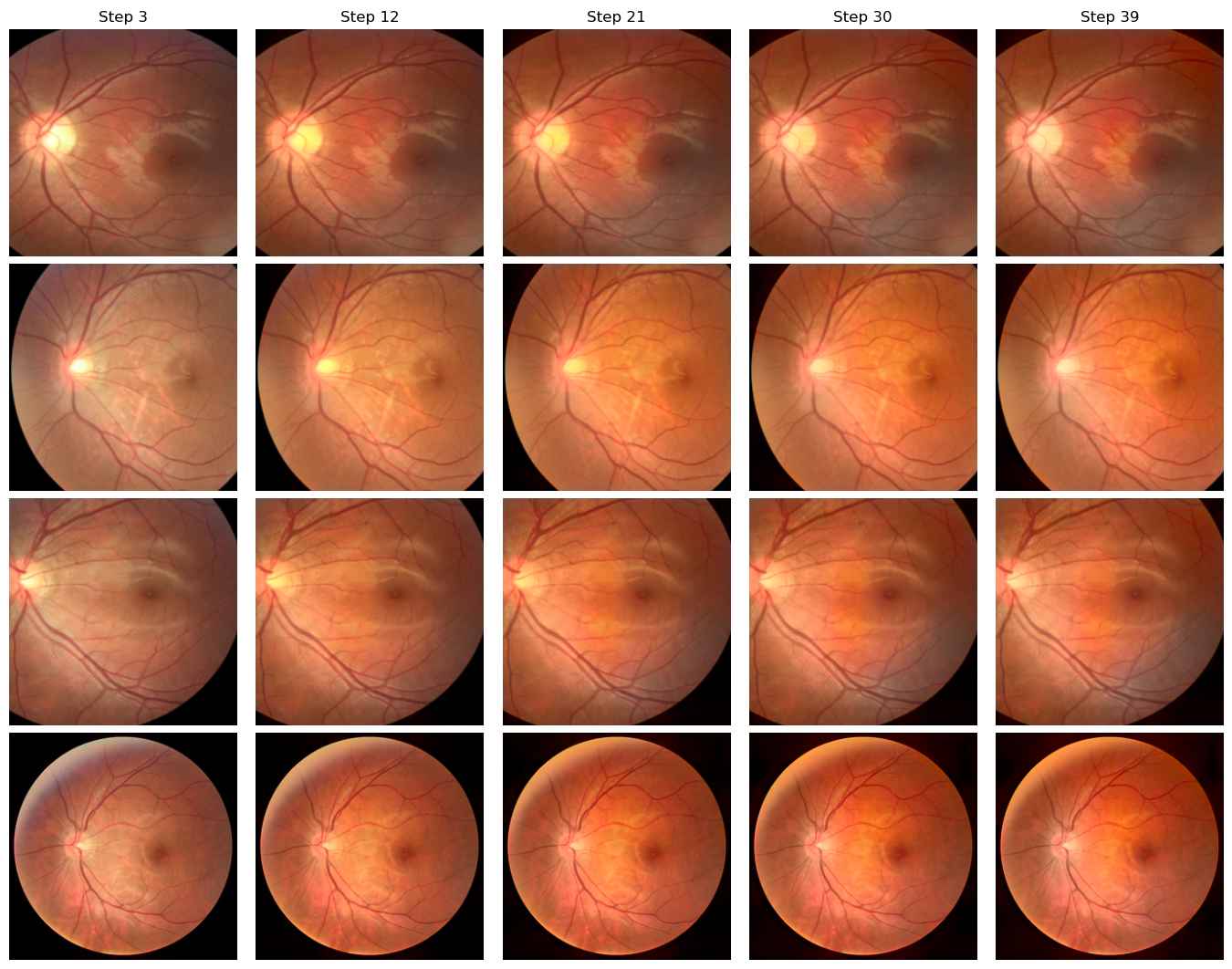
Domain D to Domain A
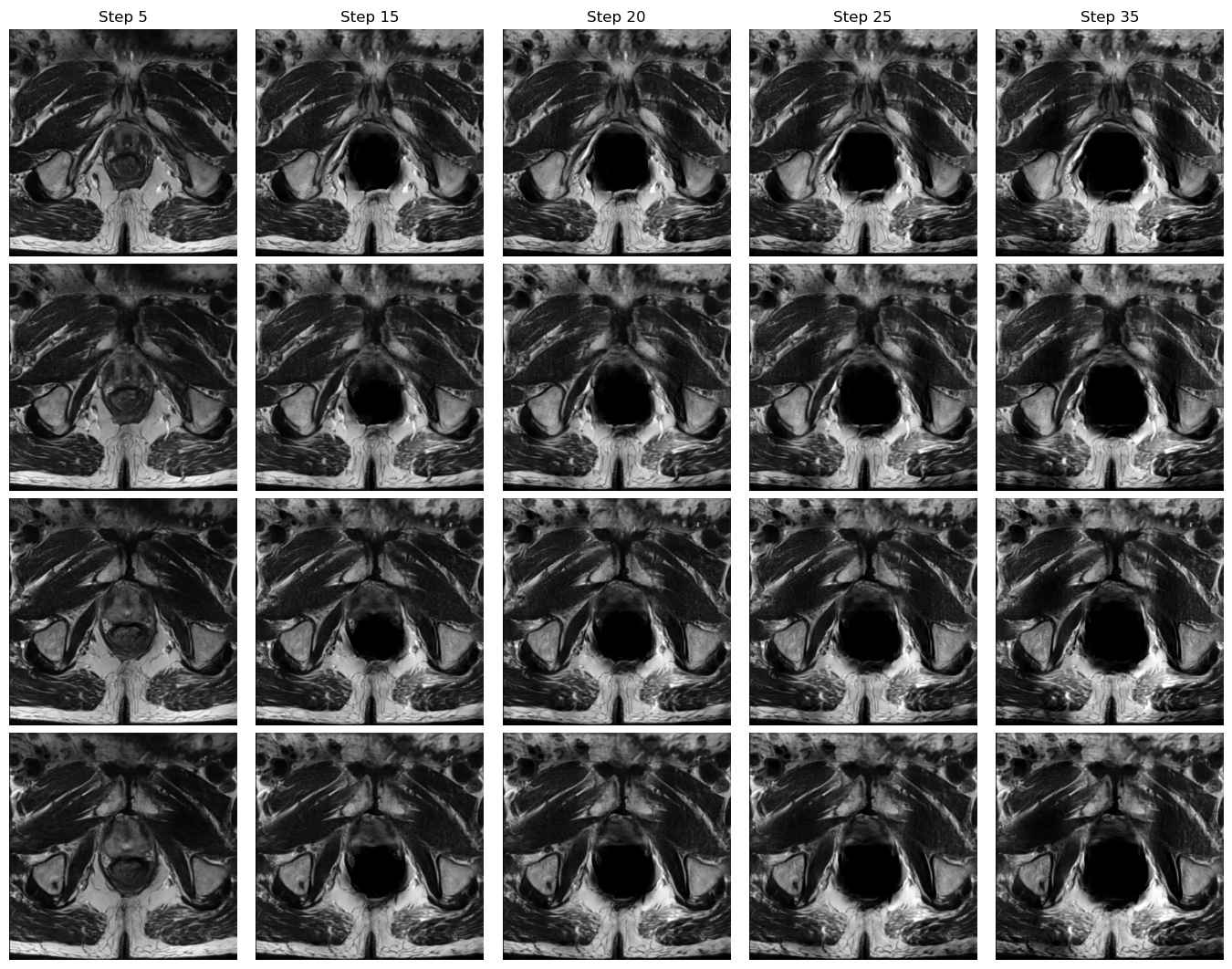
Domain A to Domain B

Domain B to Domain F

Domain C to Domain A

Domain D to Domain F
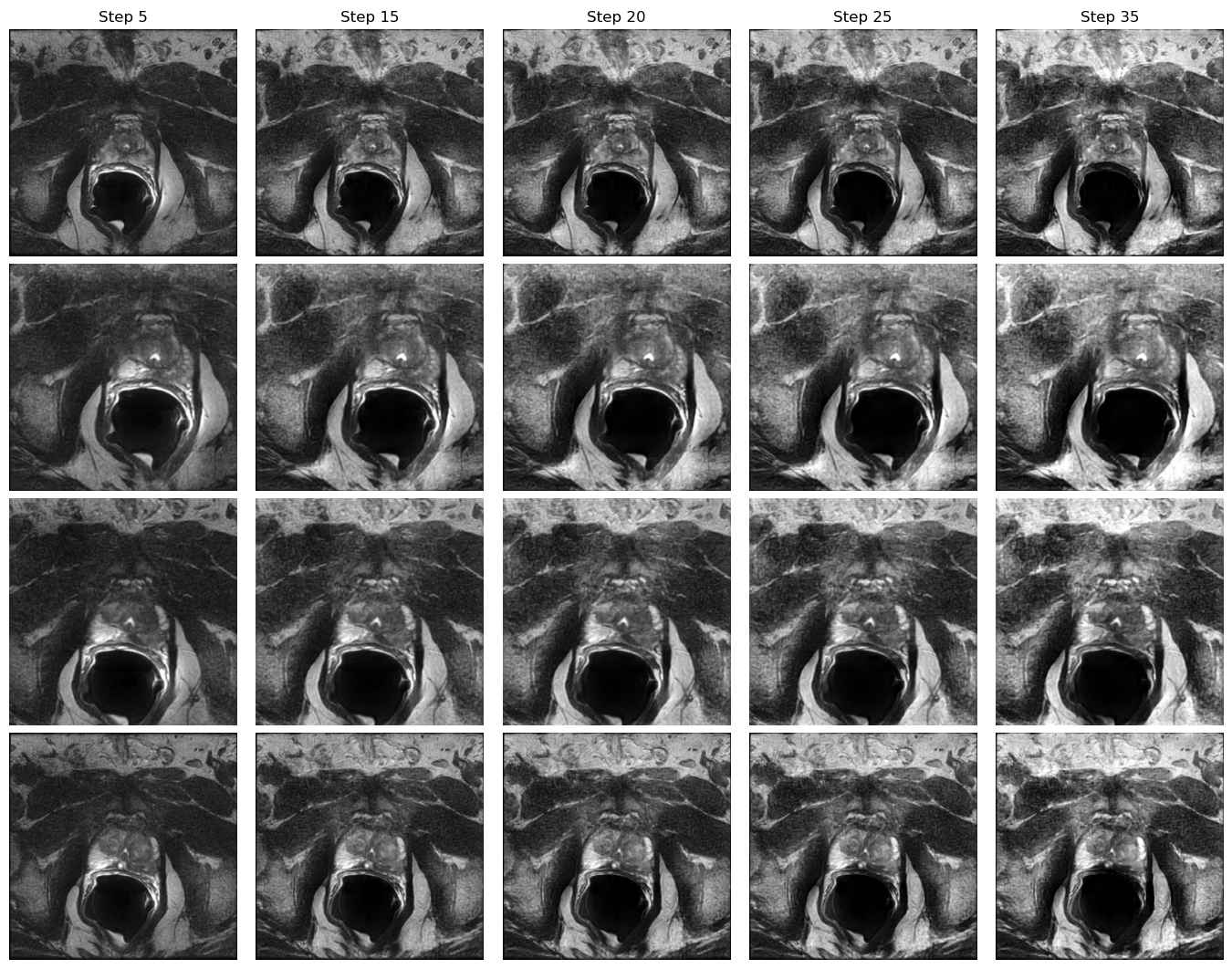
Domain E to Domain B

Domain F to Domain A
If you find this work useful, please cite:
@inproceedings{tiwary2025langdaug,
title={LangDAug: Langevin Data Augmentation for Multi-Source Domain Generalization in Medical Image Segmentation},
author={Tiwary, Piyush and Bhattacharyya, Kinjawl and Prathosh, A.P.},
booktitle={Proceedings of the 42nd International Conference on Machine Learning},
year={2025}
}