Adapt then Unlearn: Exploring Parameter Space Semantics for Unlearning in GANs

Piyush Tiwary, Atri Guha, Subhodip Panda, Prathosh A.P.
Indian Institute of Science, Bengaluru, India

TL:DR: we introduce "Adapt-then-Unlearn," a two-stage approach for removing undesired features from pre-trained GANs without requiring access to the original training data. First, the method adapts the GAN to generate only negative samples (with undesired features), then it retrains the original GAN on positive samples using a repulsion loss that pushes parameters away from the adapted model. This innovative approach successfully unlearns undesired features while maintaining generation quality, working effectively on high-fidelity GANs like StyleGAN for both class-level and feature-level unlearning tasks.

Abstract

Owing to the growing concerns about privacy and regulatory compliance, it is desirable to regulate the output of generative models. To that end, the objective of this work is to prevent the generation of outputs containing undesired features from a pre-trained Generative Adversarial Network (GAN) where the underlying training data set is inaccessible. Our approach is inspired by the observation that the parameter space of GANs exhibits meaningful directions that can be leveraged to suppress specific undesired features. However, such directions usually result in the degradation of the quality of generated samples. Our proposed two-stage method, known as 'Adapt-then-Unlearn,' excels at unlearning such undesirable features while also maintaining the quality of generated samples. In the initial stage, we adapt a pre-trained GAN on a set of negative samples (containing undesired features) provided by the user. Subsequently, we train the original pre-trained GAN using positive samples, along with a repulsion regularizer. This regularizer encourages the learned model parameters to move away from the parameters of the adapted model (first stage) while not degrading the generation quality. We provide theoretical insights into the proposed method. To the best of our knowledge, our approach stands as the first method addressing unlearning within the realm of high-fidelity GANs (such as StyleGAN). We validate the effectiveness of our method through comprehensive experiments, encompassing both class-level unlearning on the MNIST and AFHQ dataset and feature-level unlearning tasks on the CelebA-HQ dataset. Our code and implementation is available at: https://github.com/atriguha/Adapt_Unlearn.

Parameter Space Semantics

Figure 1: Illustrating linear interpolation and extrapolation in parameter space for unlearning undesired features. We observe that in the extrapolation region, undesired features are suppressed, but the quality of generated samples deteriorates.

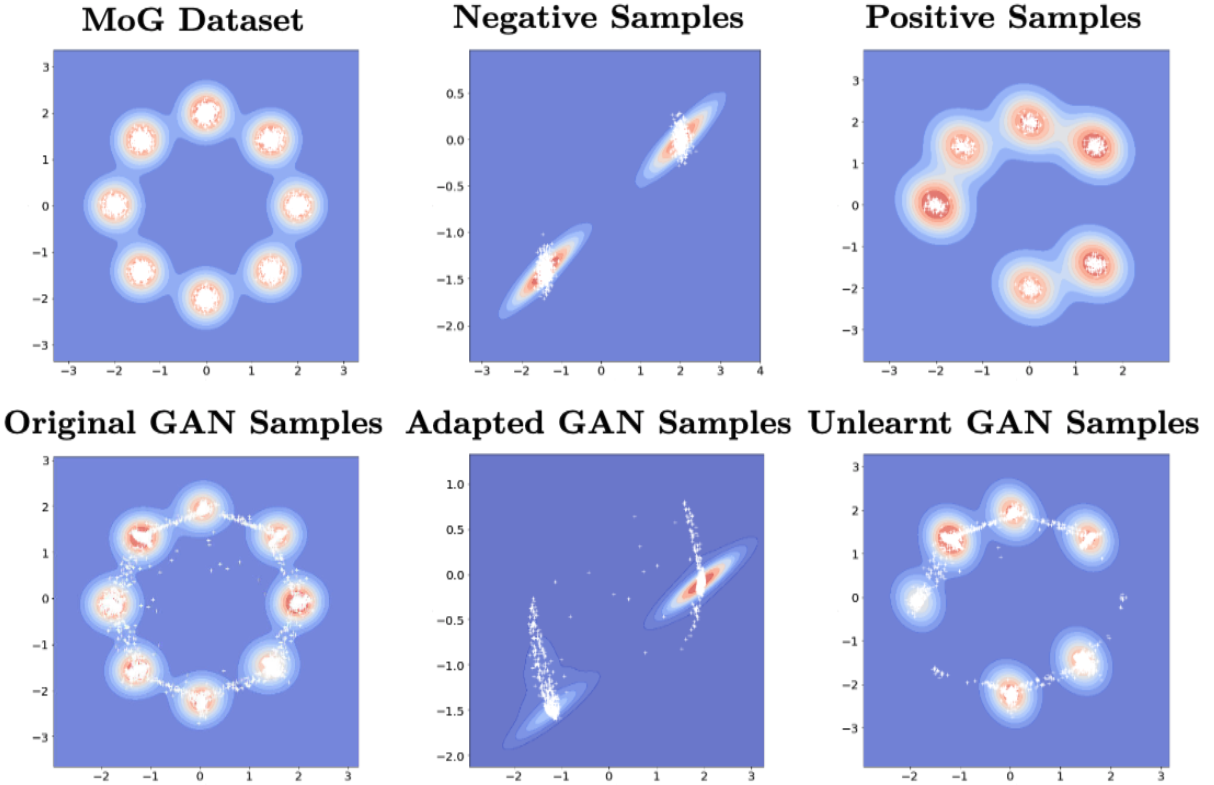
Our approach hinges in realizing interpretable and meaningful directions within the parameter space of a pre-trained GAN generator, as discussed in (Cherepkov et al., 2021; Ilharco et al., 2023). In particular, the first stage of the proposed method leads to adapted parameters that exclusively generate negative samples. While the parameters of the original pre-trained generator generate both positive as well as negative samples. Hence, the difference between the parameters of adapted generator and the paramters of original generator can be interpreted as the direction in parameter space that leads to a decrease in the generation of negative samples. Given this, it is sensible to move away from the original parameters in this direction to further reduce the generation of negative samples. This observation is shown in Figure 1. However, it's worth noting that such extrapolation doesn't ensure the preservation of other image features' quality. In fact, deviations too far from the original parameters may hamper the smoothness of the latent space, potentially leading to a deterioration in the overall generation quality (see last column of Figure 1).

Proposed Methodology

Overview of the Proposed Method

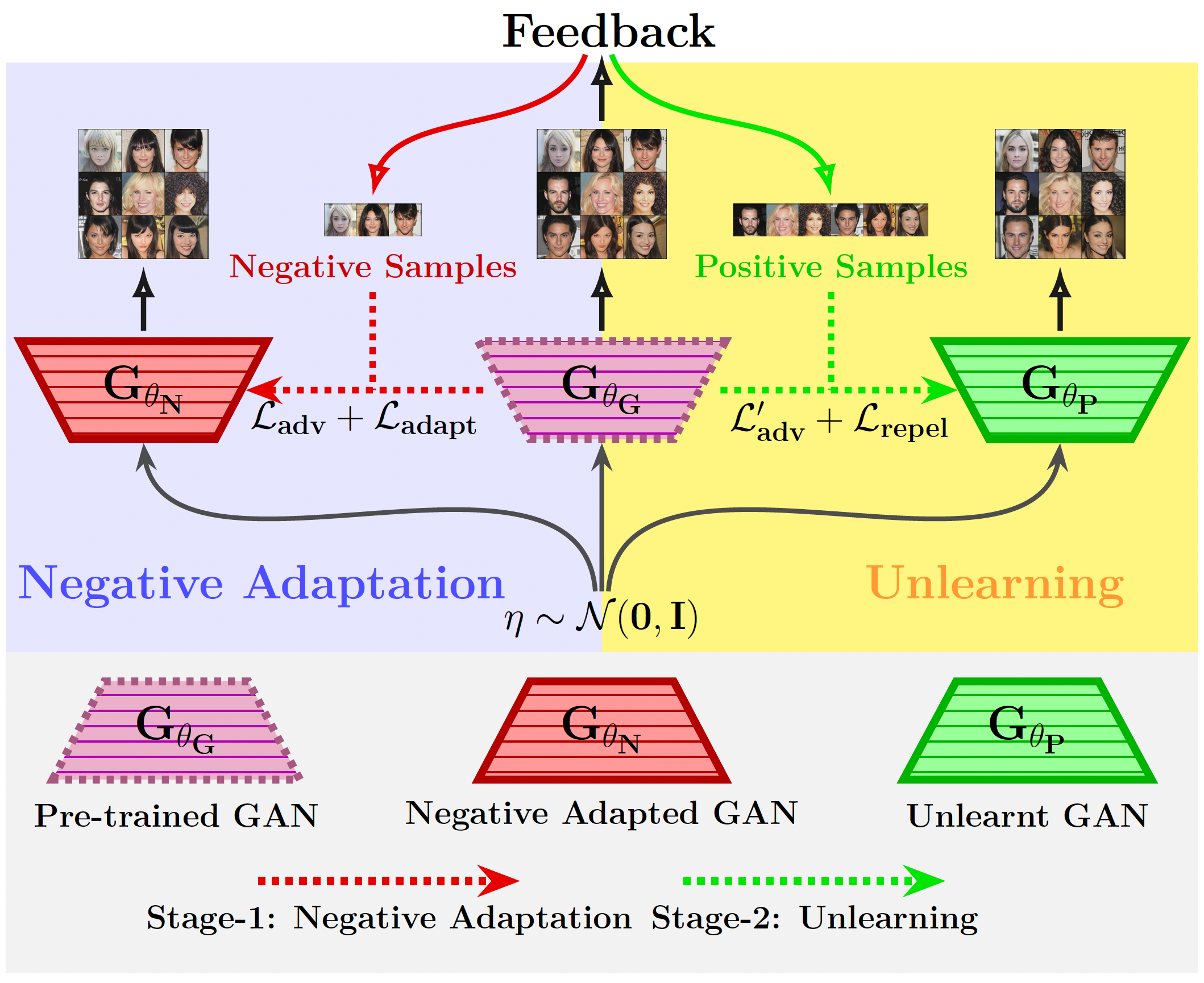
Figure 2: (left) Block diagram of the proposed method: Stage-1: Negative Adaptation of the GAN to negative samples received from user feedback and Stage-2: Unlearning of the original GAN using the positive samples with a repulsion loss. (right) An example of results obtained using our method on Mixture of Gaussian (MoG) dataset, where we unlearn two centers provided in negative samples.

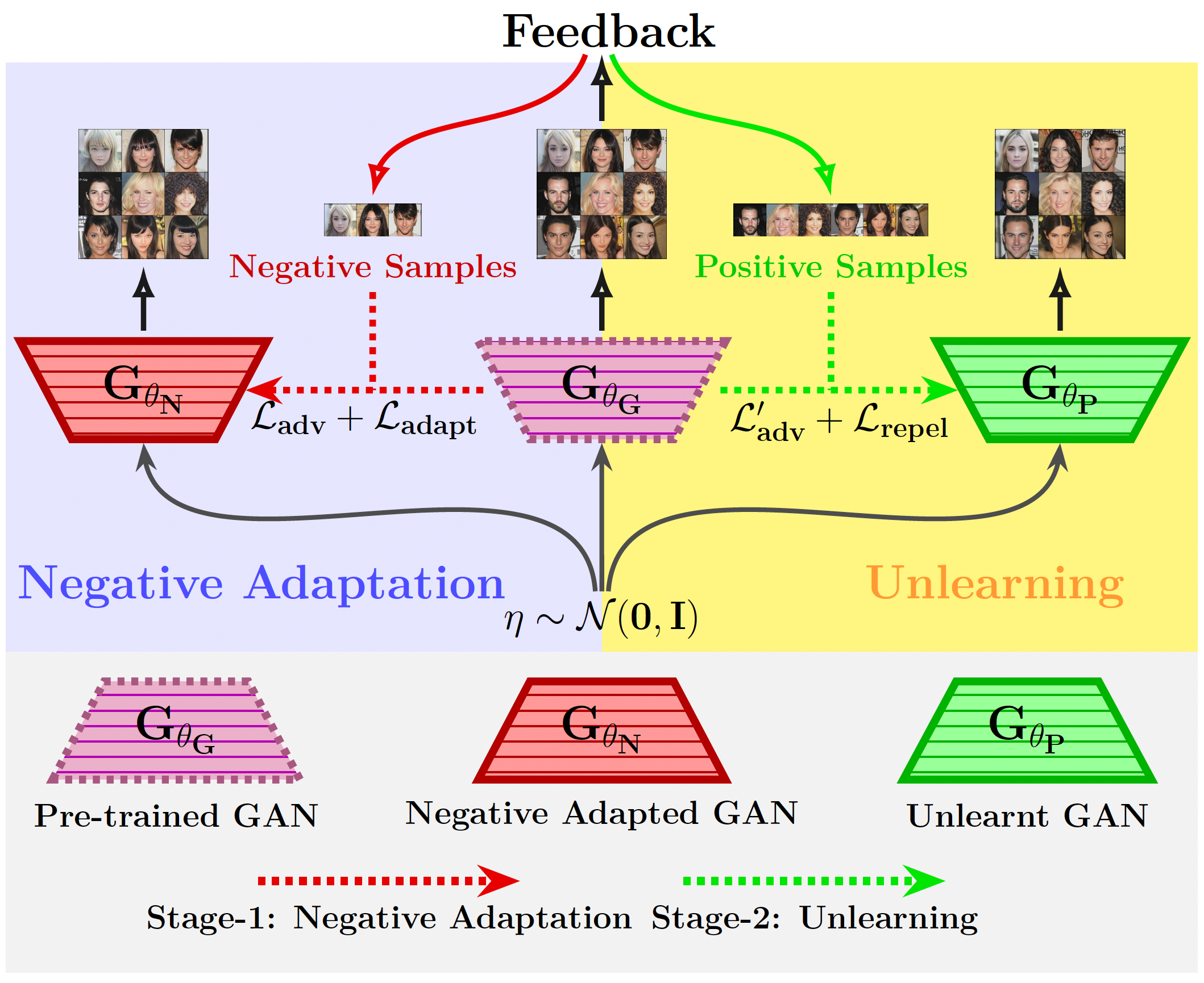
Our proposed method follows a two-stage process:

Stage 1 - Negative Adaptation: We first adapt the pre-trained GAN ($\theta_G$) using a small set of 'negative' samples provided by the user, which contain the undesired features. This results in an adapted GAN ($\theta_N$) that primarily generates these negative samples. We use techniques like Elastic Weight Consolidation (EWC) to handle the few-shot nature of this adaptation.

$$ \begin{align} \theta_N, \phi_N = \arg\min_{\theta}\max_{\phi}~ \mathcal{L}_{adv} + \gamma\mathcal{L}_{adapt} \end{align} $$ $$ \begin{align} \text{where,}~~~ \mathcal{L}_{adv} = \mathbb{E}_{\mathbf{x}\sim p_{N}(x)}\left[\log D_\phi(\mathbf{x})\right] + \mathbb{E}_{\mathbf{z}\sim p_{Z}(z)}\left[\log (1 - D_\phi(G_\theta(\mathbf{z})))\right] \end{align} $$ $$ \begin{align} \mathcal{L}_{adapt} = \lambda \sum_{i}F_i(\theta_i - \theta_{G,i}), \quad F = \mathbb{E}\left[ -\frac{\partial^2}{\partial\theta_G^2}\mathcal{L}_{\theta_G}(\mathcal{S}_n) \right] \end{align} $$

Stage 2 - Unlearning: Subsequently, we train the original pre-trained GAN using 'positive' samples (those without undesired features). Crucially, we introduce a repulsion regularizer ($\mathcal{L}_{\text{repulsion}}$) that encourages the learned model parameters ($\theta_P$) to move away from the negative parameters ($\theta_N$) obtained in Stage 1, while the standard adversarial loss ensures generation quality is maintained.

$$ \begin{align} \theta_P, \phi_P &= \arg\underset{\theta}{\min}~\underset{\phi}{\max}~ \mathcal{L}_{adv}^{'} + \gamma\mathcal{L}_{repulsion} \label{eq:objective_stage2} \\ \text{where, }\mathcal{L}_{adv}^{'} &= \underset{\mathbf{x}\sim p_{G\backslash N}(x)}{\mathbb{E}}\left[\log D_\phi(\mathbf{x})\right] + \underset{\mathbf{z}\sim p_{Z}(z)}{\mathbb{E}}\left[\log (1 - D_\phi(G_\theta(\mathbf{z})))\right] \label{eq:l_adv_stage2} \end{align} $$

Choice of Repulsion Loss

The repulsion loss ($\mathcal{L}_{\text{repulsion}}$) should encourage the learned parameter to traverse away from $\theta_N$ obtained from the negative adaptation stage. In general, one can use any function of $\|\theta - \theta_N\|_2^2$ that has a global maxima at $\theta_N$ as a choice for repulsion loss. In this work, we explore three different choices for the repulsion loss: $$ \begin{align} \mathcal{L}_{repulsion} = \begin{cases} \mathcal{L}_{repulsion}^{\text{IL2}} = \frac{1}{||\theta - \theta_N||_2^2} & \text{(Inverse $\ell_2$ loss)} \\ \mathcal{L}_{repulsion}^{\text{NL2}} = - ||\theta - \theta_N||_2^2 & \text{(Negative $\ell_2$ loss)} \\ \mathcal{L}_{repulsion}^{\text{EL2}} = \exp(-\alpha||\theta - \theta_N||_2^2) & \text{(Exponential negative $\ell_2$ loss)} \end{cases} \label{eq:repulsion-loss} \end{align} $$

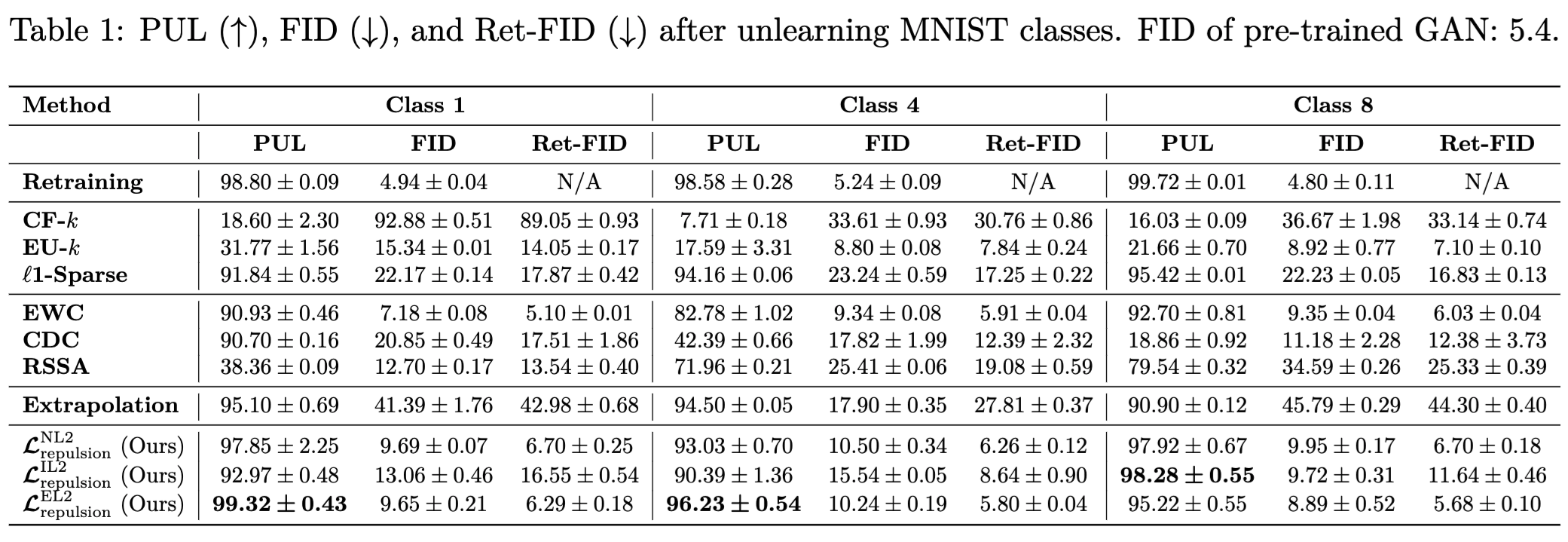
Results

Figure 3: Results of Unlearning different classes on MNIST dataset.

Figure 4: Results of Unlearning different classes on AFHQ dataset.

Figure 5: Results of Unlearning different features on CelebaHQ dataset.

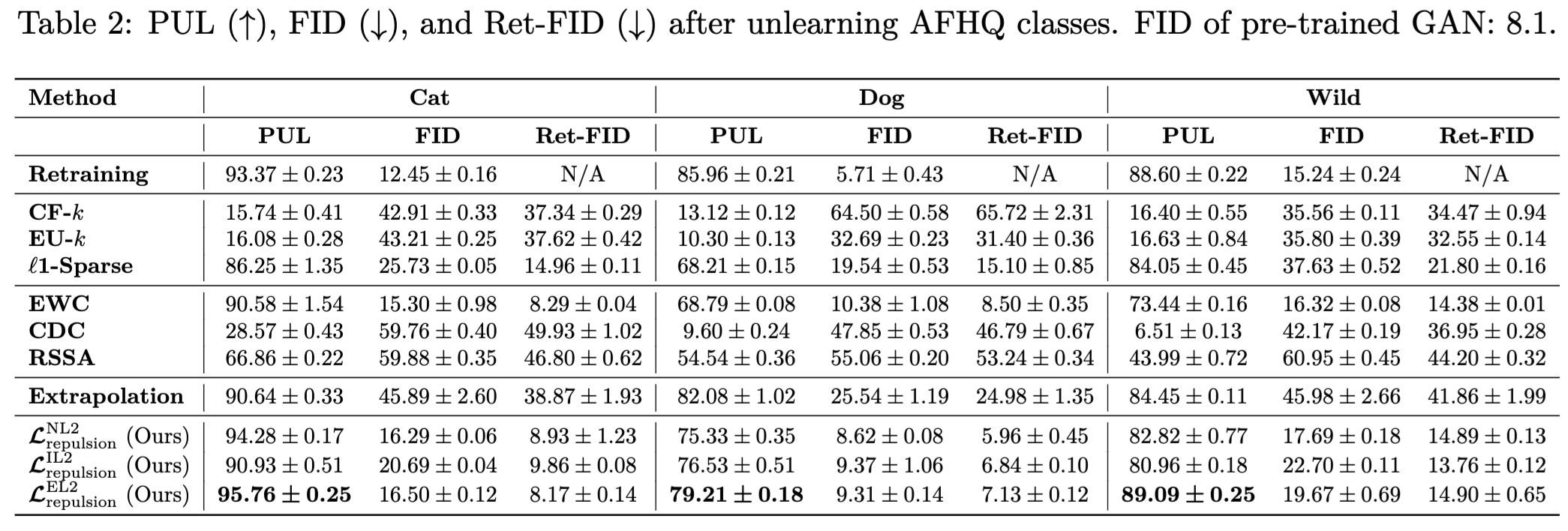
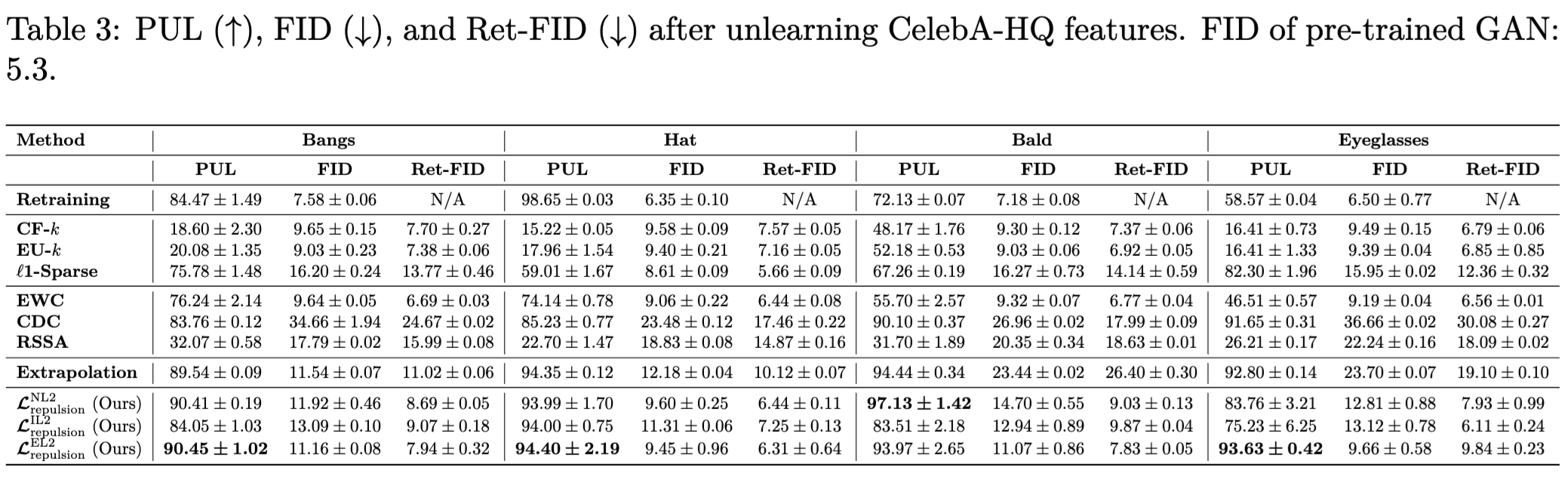
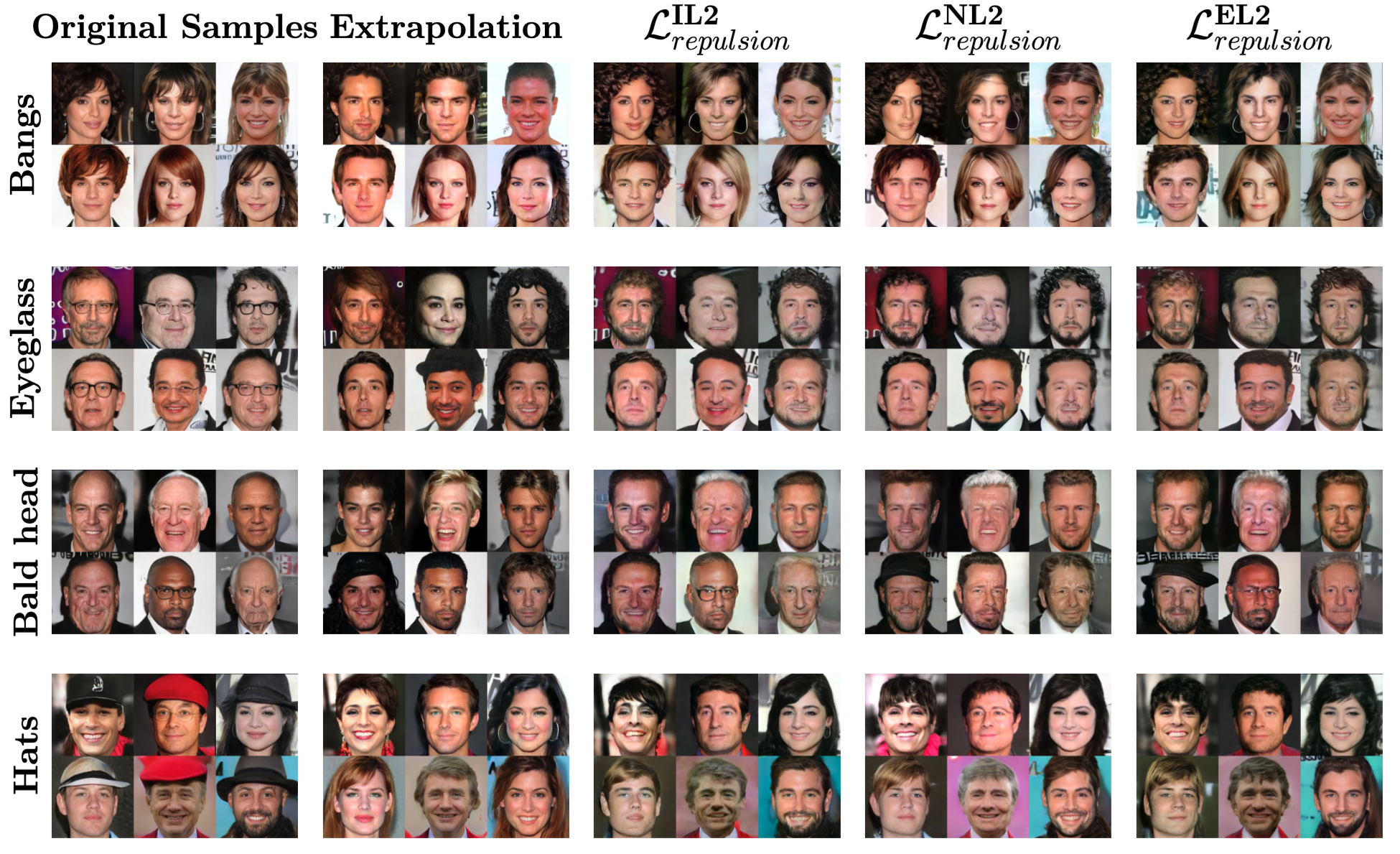
If you find our work useful, please consider citing our paper:

@article{tiwary2025adapt,
    title={Adapt then Unlearn: Exploring Parameter Space Semantics for Unlearning in Generative Adversarial Networks},
    author={Piyush Tiwary and Atri Guha and Subhodip Panda and Prathosh A.P.},
    journal={Transactions on Machine Learning Research},
    year={2025},
    url={https://openreview.net/forum?id=jAHEBivObO},
    note={Published 02/2025}
}

Piyush Tiwary, Atri Guha, Subhodip Panda, Prathosh A.P. Indian Institute of Science, Bengaluru, India